European-style options use the spot price as an input and then the internal mechanics of the model calculates the applicable forward rate, which in turn impacts the premium paid. So how does this work within the context of credit options?
Suppose I sell 10 year protection at a par spread of 100 bps and buy 5 year protection at a cost of 75 bps, both linked to the same reference entity. Ignoring fixed coupons and upfront adjustments then for the first 5 years, the two positions cancel each other out and you are left with a short protection position between years 5 and 10 (5 year protection, 5 years forward). It follows therefore that the forward starting position has a present value (PV) equal to the PV of the 10y trade less the 5y trade.
Referring back to the fourth post in this series, we know that the PV of a 10y annuity which has a notional of 1 is:
10 yr par spread x PV01 of 10 year
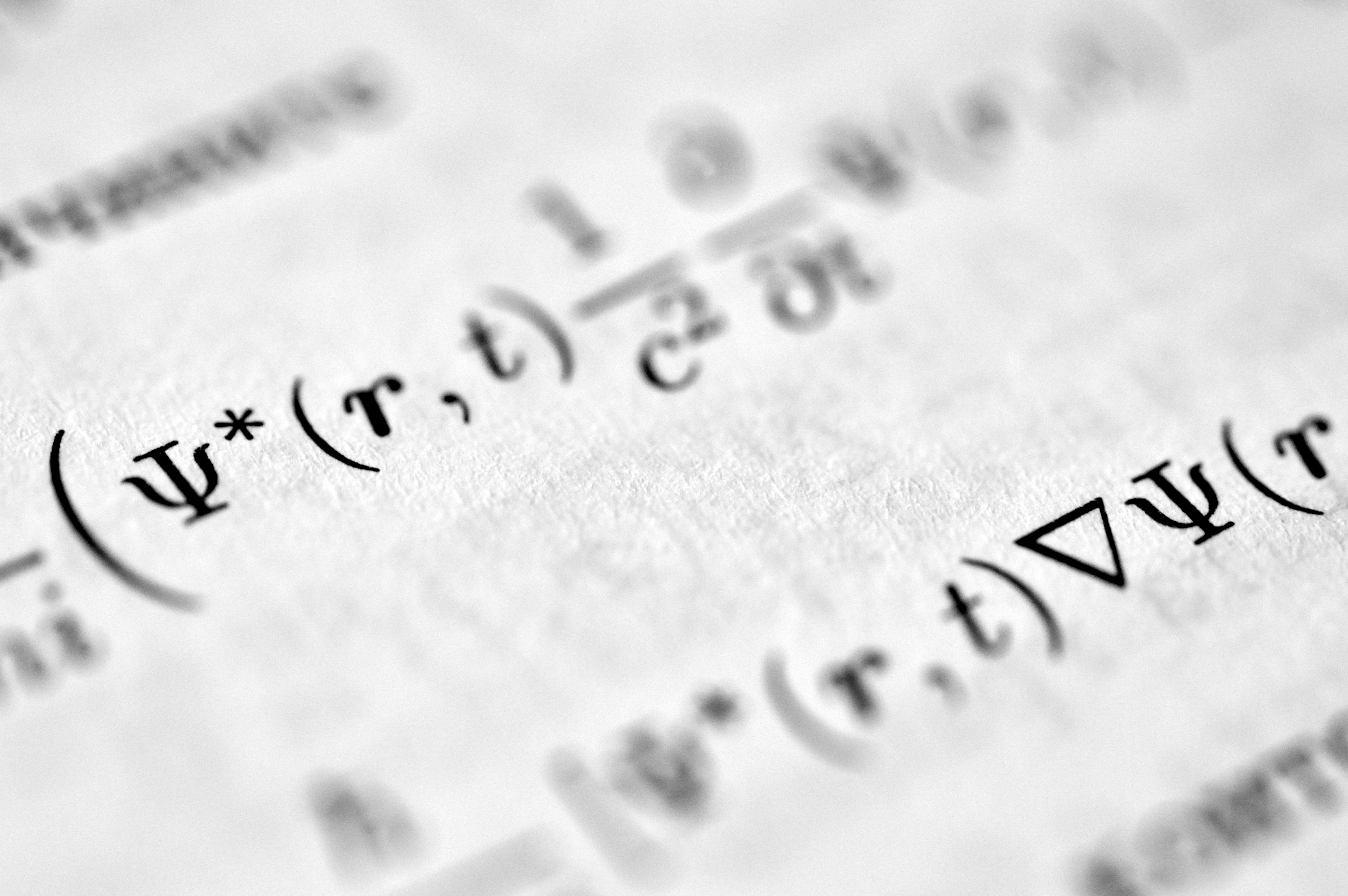
With a little bit of maths it can be shown that:
5y5y spread = (10y * PV01 of 10y) – (5y * PV01 of 5y) / (PV01 of 10y – PV01 of 5y)
So if we had a 5y CDS trading at a par spread of 75 bps and a 10 yr par spread of 100bps, if their respective PV01s were 4.5 and 8.5, the forward spread for a credit option would be:
(100 x 8.5) – (75 x 4.5) / 8.5 – 4.5 = 128 bps.

