Introduction
In some previous posts I had explained the concept of delta and gamma within an option trading context. One of the strategies we analyzed was a delta-hedged short call position. This position has characteristics similar to a classic “straddle” position. A short straddle is constructed as ell a call and a put with the same strike and maturity.
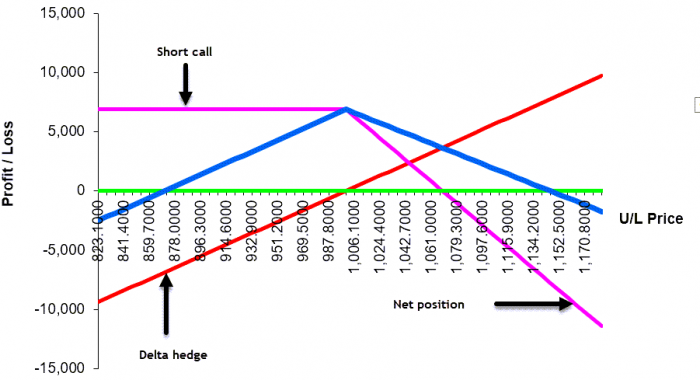
One of the conclusions was that such a strategy would lose money if the market experienced “significant” price movements. This is because the delta hedging activities would generate a loss on the position.
Short volatility trade – the motivation
In this post we ask the question, why would anyone execute such a trade? By selling the option, the trader will generate an initial premium. However, this is not their profit as this could be eroded by delta hedging losses. Only upon the termination of the position would the profit be realised. So what could contribute to a profitable position? The passage of time provides us with one answer.
Theta
According to option theory, every day that the option position is open its value will diminish. Theta is the the amount by which the option position will change as a result of a 1 day passage of time. For those new to options, the notion that a reducing value of an asset contributes to a profit may seem counterintuitive. But to close out the position the trader would need to execute an equal and opposite position. So if they have sold a call, they need to buy a call. If the cost of buying the call has fallen as a result of time, this means they will pay out a smaller out to terminate the exposure. As a result they will show a profit.
So this gives us our trade rationale. Such a “short volatility” trade requires the option trader to believe that the passage of time will generate a greater profit than the losses incurred from delta hedging activities.
Suppose we value a 1 year ATM call option on Tesla based on a share price of $750 and an implied volatility of 20%. The premium comes out at $180, which is all time value. All other things being equal, the option will have zero value at expiry and so the loss will be equal to the premium. If we were to analyse the option after 6 months, it would have a value of $127 and will have lost about 29% of its value.
If we were to repeat the exercise with an OTM call option (strike = $1,100) the initial premium would be $86. After 6 months the option’s value would be $38 and so it will have lost $48 or about 56% of its value.
Conclusion
What does this tell us? The dynamics of losses as a result of the passage of time will vary according to the relative “moneyness” of the option. Those options with the lowest premiums (i.e., OTM options) will lose their value fastest. However, in absolute terms the ATM option will lose incur the greatest monetary loss.

